
Projects
GPU-accelerated Poisson Solver
SASE: Caroline Cardinale (Division of Engineering and Applied Science), SASE GRA Fellow
The Poisson equation arises in diverse fields, including electrostatics, gravitation, and incompressible fluid flow. In fluid simulations, it appears in the projection step of the Navier–Stokes equations, where a scalar Poisson equation is solved for the pressure field. This step becomes the computational bottleneck, as traditional discrete Poisson solvers scale quadratically with the number of grid points. For large-scale three-dimensional computations, this quickly becomes intractable.
To address this, the Colonius group in EAS developed the fast lattice Green’s function (FLGF) method [1,2], a fast multipole-like approach that achieves linear complexity by leveraging the regularity of the underlying uniform Cartesian grid. This allows for efficient equidistant interpolation and FFT-based blockwise convolutions. Our current CPU-based implementation exhibits excellent strong and weak scaling; however, it is limited to CPU clusters.
Through the Schmidt Academy, we aim to first accelerate FLGF using GPUs and then to prepare the codebase for open-source release. The open-source effort will modernize the build system, improve portability through Docker, and implement automated testing and documentation. The long-term goal is to establish a robust foundation for GPU-accelerated Poisson solvers. Software engineering expertise will be critical for addressing challenges such as data transfer overhead, efficient parallelization, and a smooth transition to an open-source platform.
The FLGF forms the backbone of our external flow solver, NS-LGF-AMR [3], which simulates the incompressible Navier–Stokes equations in free-space and around rigid, accelerating bodies. GPU acceleration of FLGF will directly speed up this solver, enabling simulations at higher Reynolds numbers and the exploration of new flow regimes. For my thesis, this will allow for a deeper understanding of vortex bifurcations and turbulence onset in biologically inspired delta wings.
Beyond my own work, a GPU-accelerated, open-source FLGF solver is a valuable tool for the broader CFD and physics communities, enabling faster, more scalable Poisson solves across diverse applications, from turbulence to electrostatics.
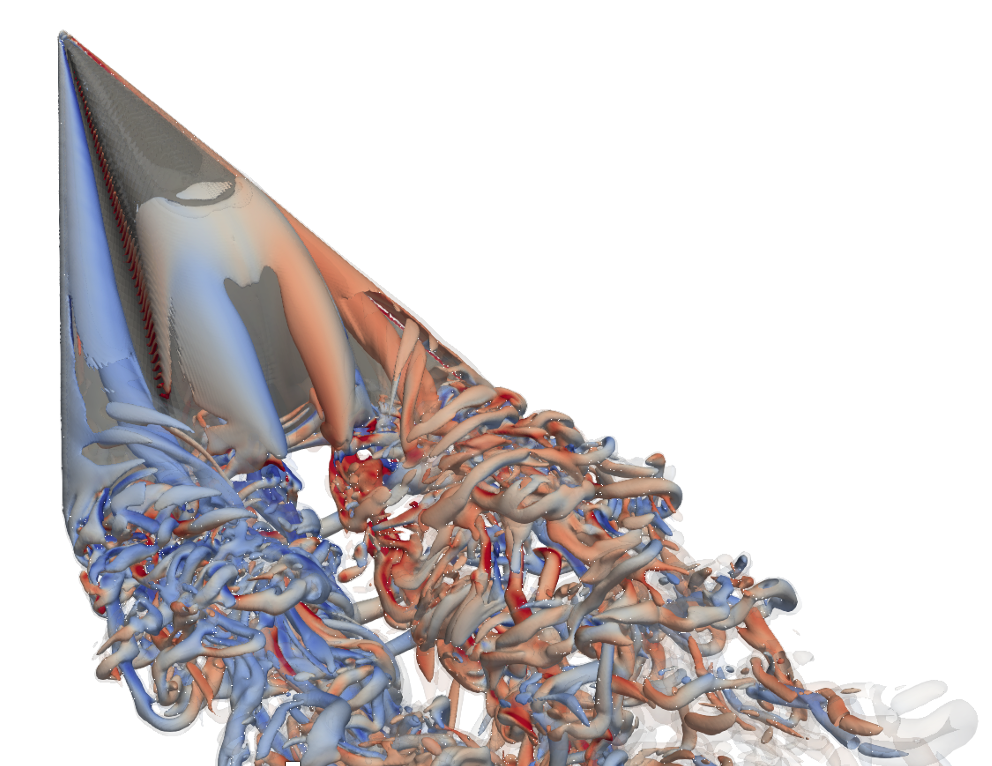
Figure: Flow past a boxfish-inspired delta wing. Q-criterion isosurfaces are shown, colored according to axial vorticity.
[1] S. Liska and T. Colonius, “A parallel fast multipole method for elliptic difference equations,” Journal of Computational Physics, vol. 278, pp. 76–91, 2014.
[2] B. Dorschner, K. Yu, G. Mengaldo, and T. Colonius, “A fast multi-resolution lattice green’s
function method for elliptic difference equations,” Journal of Computational Physics, vol. 407, p. 109 270, 2020.
[3] K. Yu, B. Dorschner, and T. Colonius, “Multi-resolution lattice green’s function method for incompressible flows,” Journal of Computational Physics, vol. 459, p. 110 845, 2022.